| joelbchristian.com |

| Joel B Christian P.E. registered professional engineer |

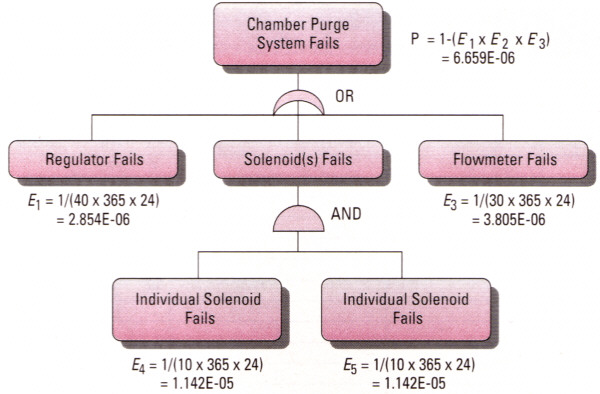 (1)
(1)
| The probability of 1/1000 is in many sources, one being: collected data reported in Table 4 & Table 5, Page 849, "Evaluation of Human Work, 3rd Edition", Eds John R. Wilson, and Nigel Corlett. CRC Press (2005). |
| Contact Info |